Red Black Trees (1)

From now on, I will refer to a red black tree as a RBT. The complete code can be found at RBT2.java and rbt.py.

put()

Adding a new key to a RBT is generally the same with the algorithms for a regular BST. But a fix-up step insert-fixup() is required because modifying would violate the red-black tree properties.

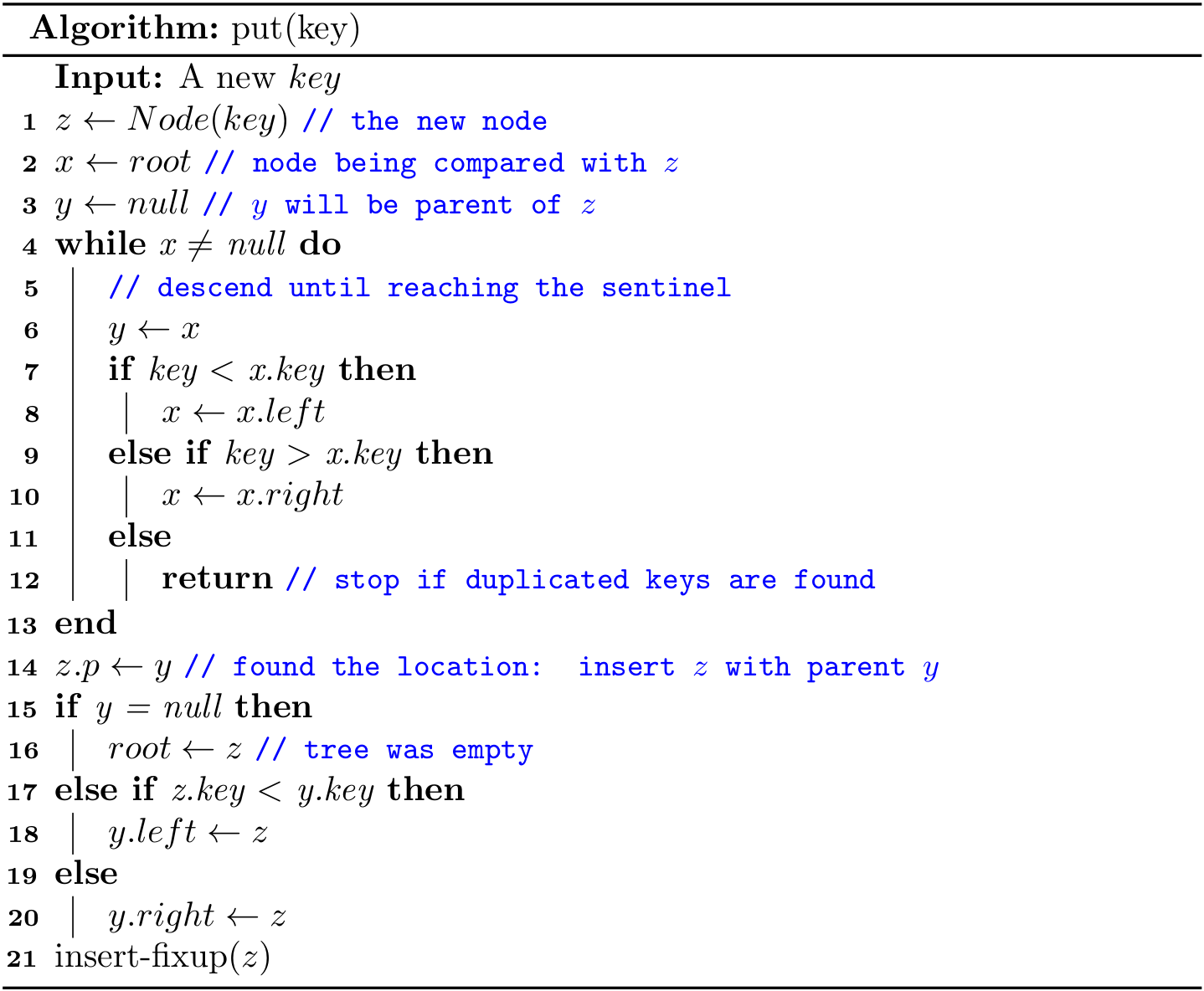
For a newly created node, its color is RED by default.

public Node(Key key) {
    this.key = key;
    color = RED;
    left = null;
    right = null;
    p = null;
}

To understand how insert-fixup() works, we shall first determine which violations of the red-black properties might arise upon inserting node z and coloring it red.

insert-fixup()

What violations of the red-black properties might occur?

• Case a: If z is the root, then it violates Property 2. The solution to this is naive: just re-color it to BLACK.
• Case b: If z is not the root, and its parent is also colored in RED, then it violates Property 4. The solution to this is a bit complicated.

In describing the structure of a RBT, we’ll often need to refer to the sibling of a node’s parent. We use the term uncle for such a node. The following figures show insert-up() operates on a sample RBT, with cases depending in part on the colors of a node, its parent, and its uncle.

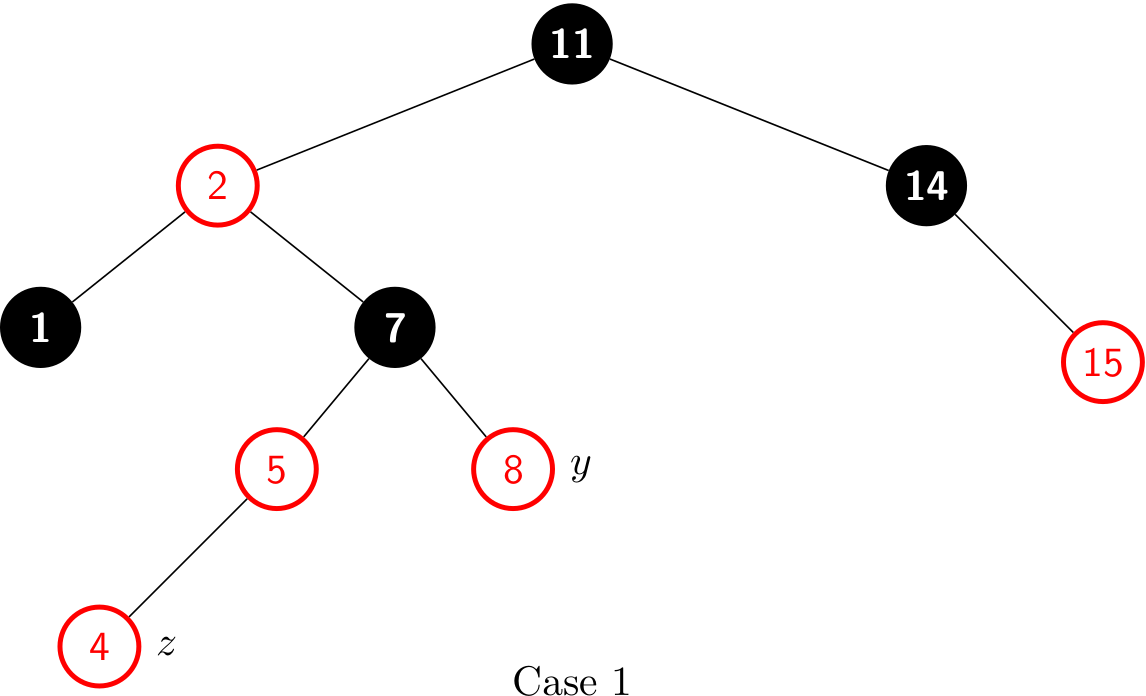
Case 1 violates Property 4 after a node z is inserted. After re-coloring, it becomes:

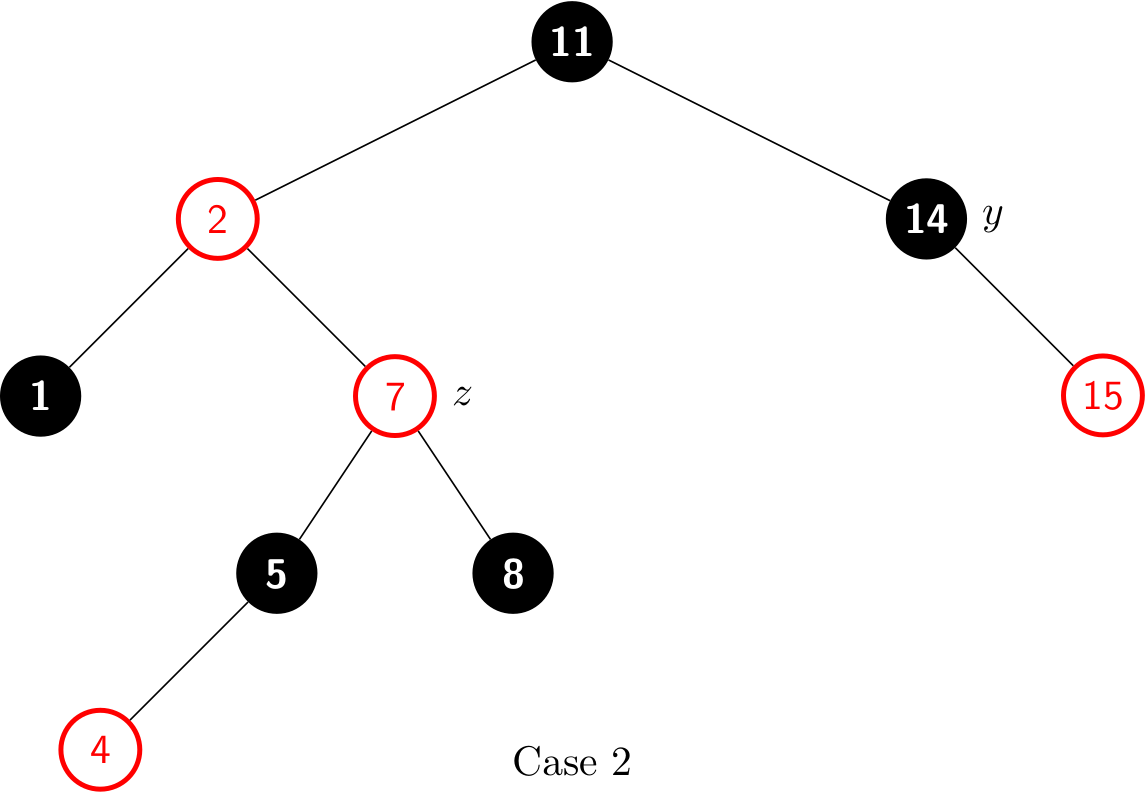
Case 2 also violates Property 4. After a left rotation, it becomes:

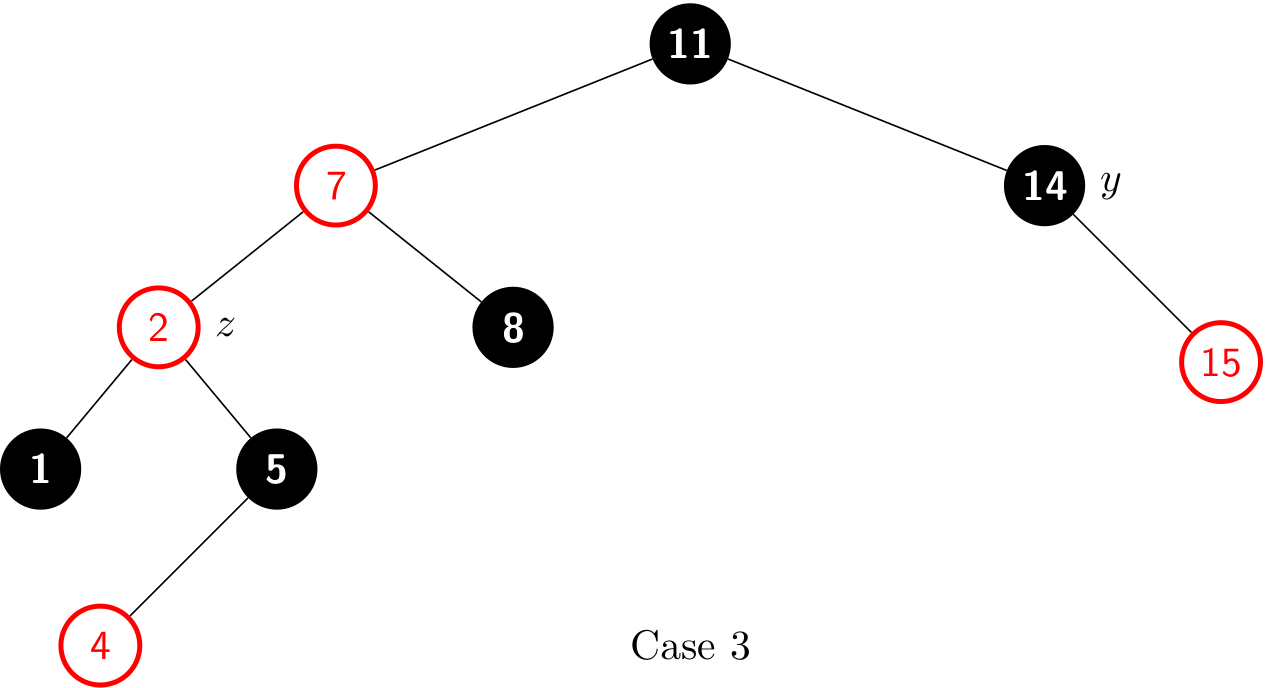
Case 3 also violates Property 4. After a right rotation, it becomes a legal RBT:

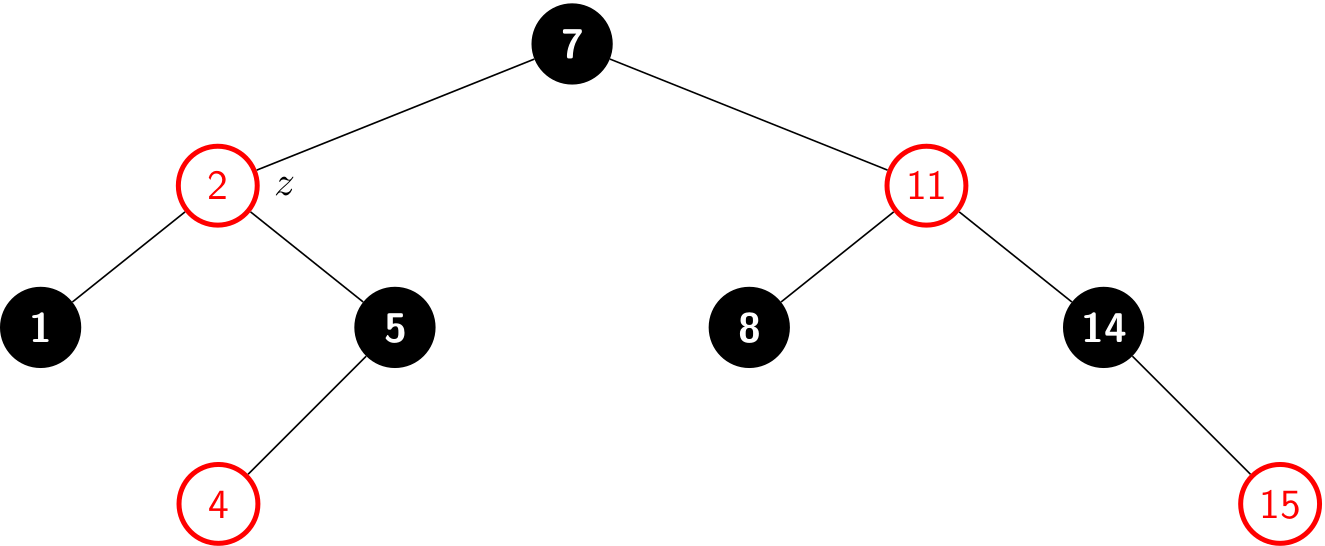
The three cases above show the operations when z's parent is a left child. And if z's parent is a right child, there are another three cases with "right" and "left" exchanged.

We can use the helper methods to access the parent, left, right and color of a node x. For example, z.p.p.left can be written as leftOf(parentOf(parentOf(z))). However, it is safe to use z.p.p.left directly. Because if z.p.color is RED, then z's grandfather (i.e., z.p.p) always exists.

By the way, it does not make sense to assign a color to null, so we can use the following helper method to set the color for a given node:

private void setColor(Node<Key> x, boolean c) {
    if (x != null) {
        x.color = c;
    }
}

Maintenance

There are six cases within the while loop, but we'll examine only the tree cases in lines 2-23, when z's parent z.p is a left child of z's grandparent z.p.p. The proof for lines 21-41 is symmetric.

Case 1 differs from cases 2 and 3 by the color of z's uncle y. If y is red, then case 1 executes. Otherwise, control passes to cases 2 and 3. In all three cases, z's grandparent z.p.p is black, since its parent z.p is red, and Property 4 violated only between z and z.p.

Case 1: z's uncle y is red

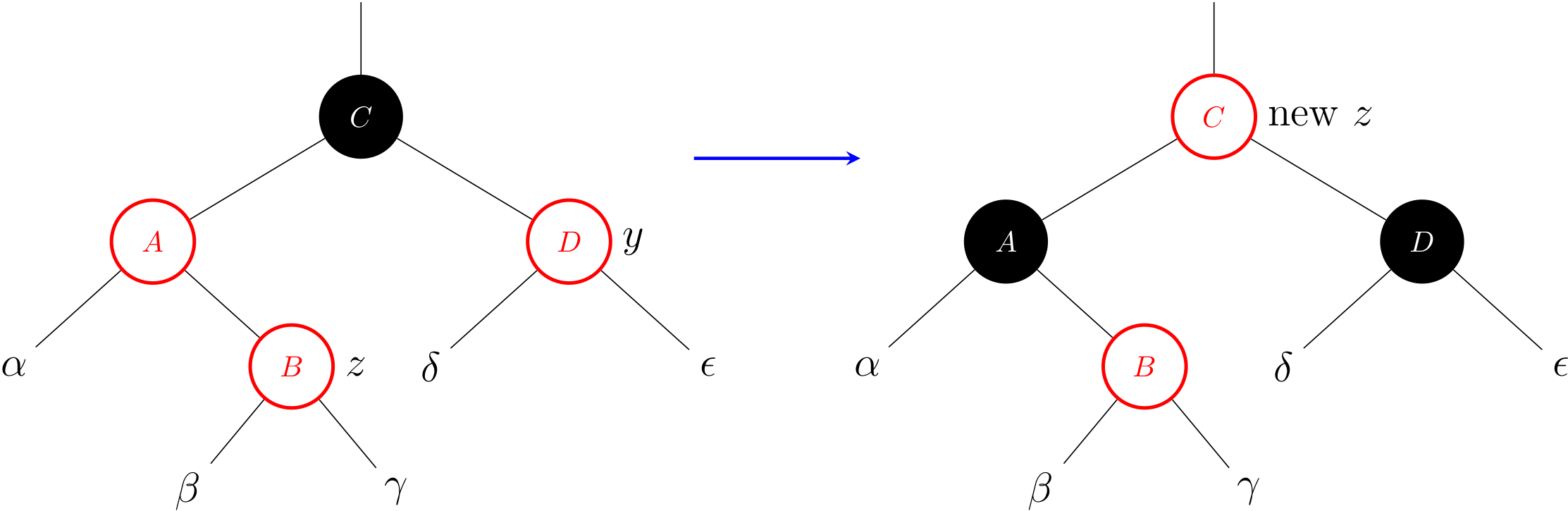
The figure above shows the situation for case 1, which occurs when z, z.p and y are red. In fact, the same action occurs regardless of whether z is a right child or z is a left child.

Because z's grandparent z.p.p is black, its blackness can transfer down one level to both z.p and y, thereby maintaining Property 5. Then, the pointer z moves up two levels in the tree.

Case 2: z's uncle y is black and z is a right child

Case 3: z's uncle y is black and z is a left child

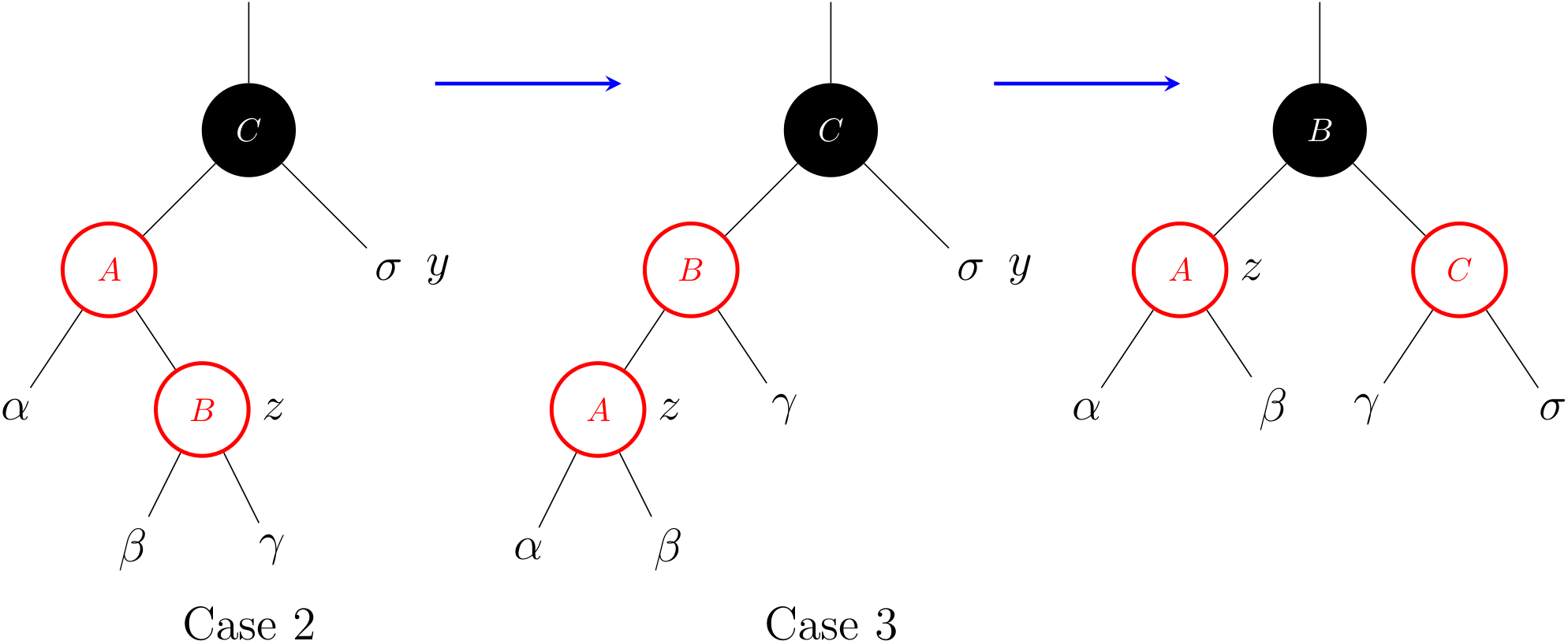
As we can see, a left rotation immediately transforms case 2 into case 3. Case 3 performs some color changes and a right rotation. At this point, there are no longer two red nodes in a row.