Direct-address Tables
Direct addressing is a simple technique that works well when the universe U of keys is reasonably small. Suppose each element has distinct key drawn from the universe \(U = \{0, 1, \dots, m - 1\}\), where m is not too large.
To represent the dynamic set, you can use an array, or direct-address table, denoted by T[0:m-1], in which each position, or slot (a.k.a., bucket), corresponds to a key in the universe. Slot k points to an element in the key k. If the set contains no element with key k, then T[k] is null.
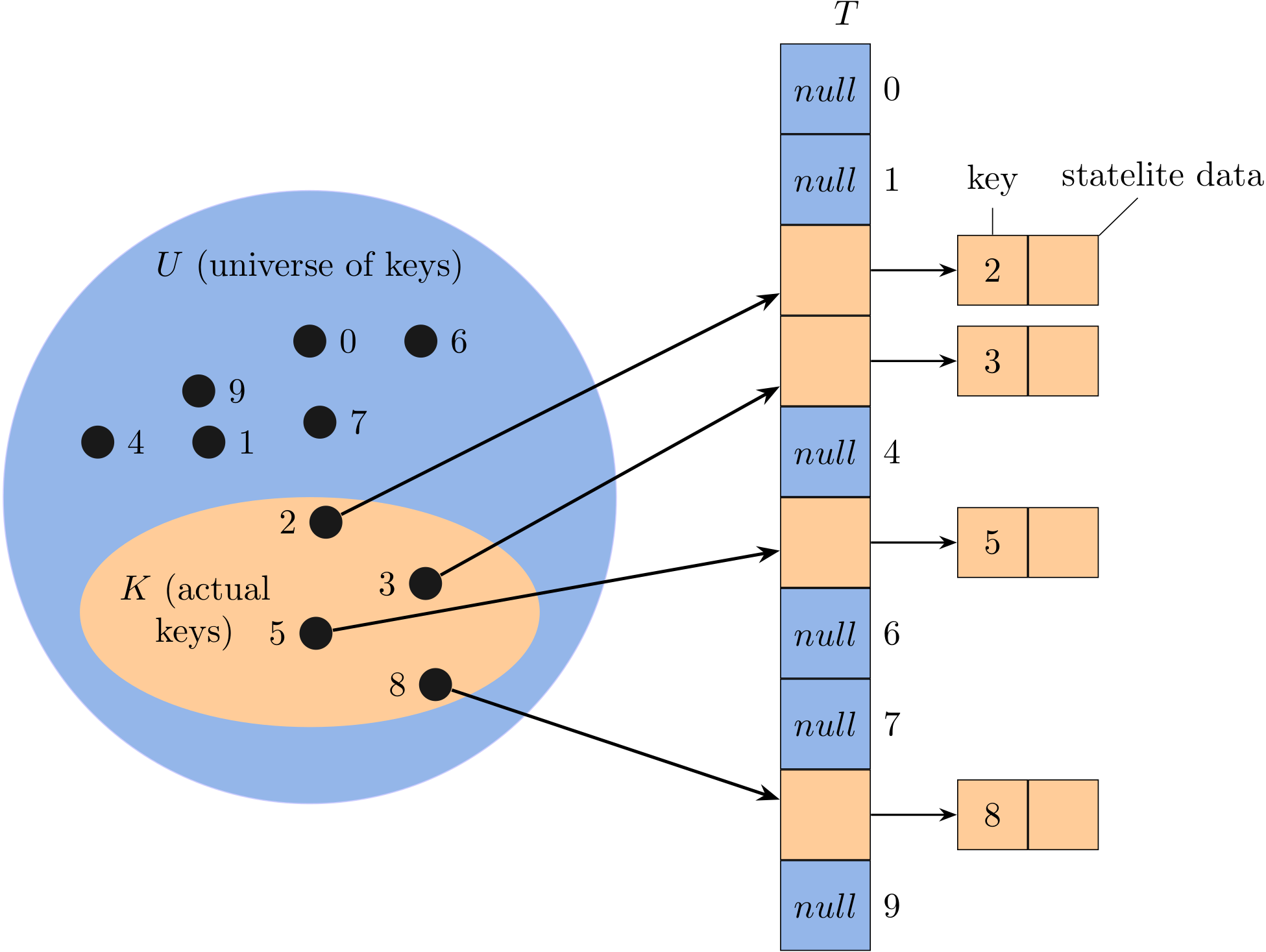
The set \(K = \{2, 3, 5, 8\}\) of actual keys determines the slots in the table that contain pointers to elements. The other slots, in blue, contain null. For some applications, the direct-address table itself can hold the elements.
The three dictionary operations based on a direct-address table are trivial to implement as long as you are able to use an array. The key point is to remember: the index of the object is its key.
def direct_address_search(self, k):
return self._t[k]
def direct_address_insert(self, x):
self._t[x.key] = x
def direct_address_delete(self, x):
self._t[x.key] = None