Queues in Python
An implementation of our Queue API based on the list data structure is also straightforward.
class Queue:
"""A first-in, first-out (FIFO) data structure."""
def __init__(self):
self._data = []
def size(self):
return len(self._data)
def is_empty(self):
return len(self._data) == 0
def enqueue(self, item):
self._data.append(item)
def dequeue(self):
if self.is_empty():
raise NoElement('Dequeue from empty queue!')
return self._data.pop(0)
Note that the dequeue() is based on pop() with index 0 as the parameter, meaning popping the first element from the list.
Iterator
The iteration over a queue is like iterating a list, so we can reuse the iterator of the list:
def __iter__(self):
return iter(self._data)
We do not have to implement the __next__ method manually. By taking leveraging of iterators, we can use the following for statement:
q = Queue()
q.enqueue(1)
q.enqueue(9)
q.enqueue(4)
q.enqueue(9)
for i in q:
print(i)
The complete code can be found at queue.py.
Time complexity
The following table summerizes the queue's time complexity:
| Operation | Running time |
|---|---|
| enqueue() | \(O(1)\) |
| dequeue() | \(O(N)\) |
| is_empty() | \(O(1)\) |
| size() | \(O(1)\) |
As we can see, most operations, except for dequeue() are with constant time complexity1, so it is very efficient. However, the dequeue() is inefficient as it grows linearly with respect to the size of the queue (i.e., N).
To validate this theoretical analysis, I design a simple benchmark to test the performance (see queue_vary_size() method in benchmark.py). The main idea is summarized in the following:
- Initialize queues with different size (1000000, 2000000, 3000000, 4000000, 5000000).
- Perform the
dequeue()operation, and time it2.
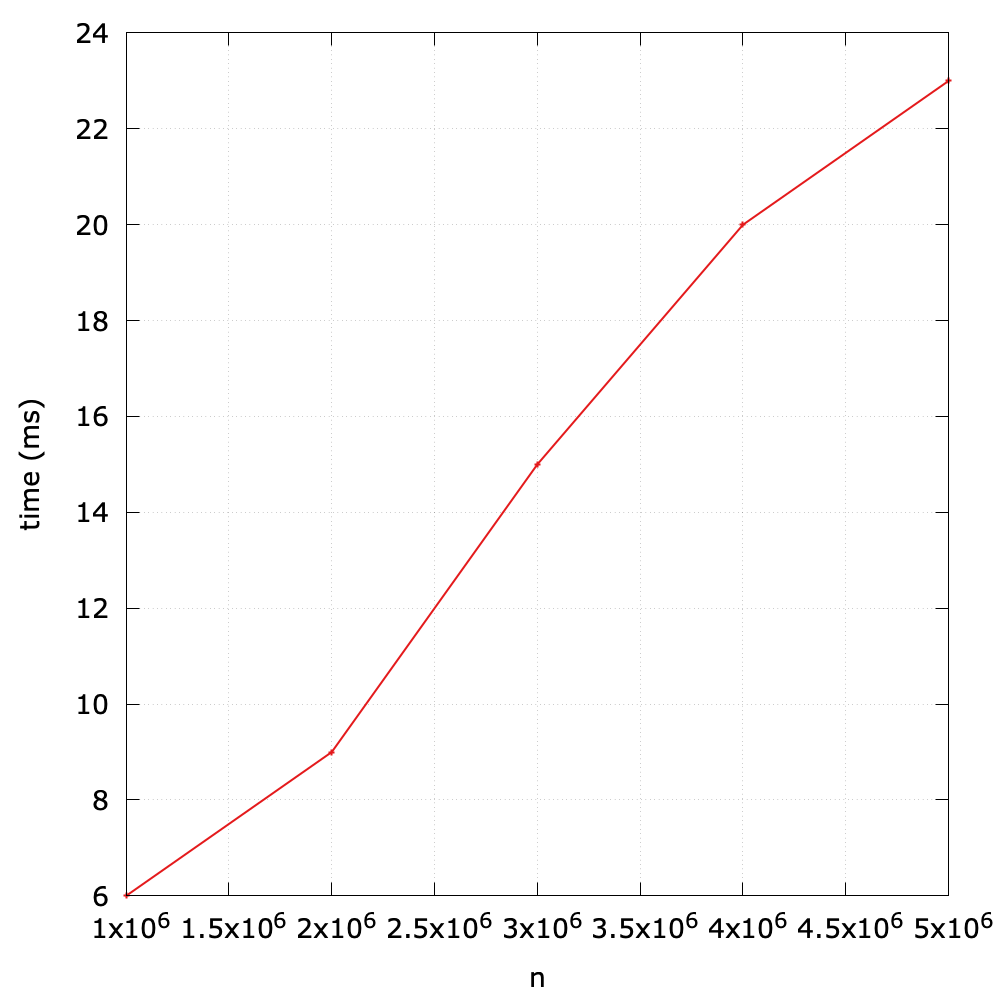
As we expect, the running time is roughly linear with respect to the size of the queue.
Now let's explore the reason of the inefficiency. Since the underlying data structure is a list, when we call enqueue() on it, the first item will be removed and the next N-1 items will be shifted to the left. Clearly, this moving action will result in \(O(N)\). Of course this design still achieves an acceptable performance in applications in which queues have relatively modest size, but when it comes to a large amount of data, it should be improved.
Using an array circularly
This subsection is adapted from Circular Queue. Such structure is also known as ring buffer in many applications.
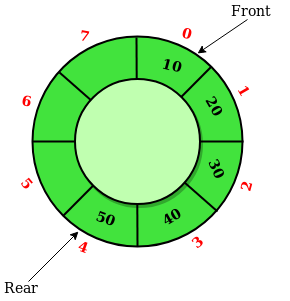
As illustrated in the figure above, we shall maintain a front pointer (i.e., index) to point to the first item and use rear pointer (i.e., index) to point to next available position3. Assume this circular array is large enough to hold all items:
enqueue(): update rear to next one in the clock-wise.dequeue(): update front to next one in the clock-wise.
Now let's consider a running example to understand the principle of circular arrays. Suppose the size of the array is 8, and the queue q is empty at start, and the front is 0:
| Operation | Front | Rear | Size |
|---|---|---|---|
| (Start) | 0 | 0 | 0 |
| q.enqueue(10) | 0 | 1 | 1 |
| q.enqueue(20) | 0 | 2 | 2 |
| q.enqueue(30) | 0 | 3 | 3 |
| q.dequeue() | 1 | 3 | 2 |
| q.enqueue(40) | 1 | 4 | 3 |
| q.enqueue(50) | 1 | 5 | 4 |
| q.dequeue() | 2 | 5 | 3 |
Obviously, the dequeue() operation only results in a pointer shift, so the time complexity is \(O(1)\). What a clever design! In addition, we can find that the specific pointer (i.e., index) does not really matter, so we can maintain front and size instead, and the rear can be computed based on them.
class CircularQueue:
"""A queue based on a circular array."""
DEFAULT_CAPACITY = 10
def __init__(self):
self._data = [None] * CircularQueue.DEFAULT_CAPACITY
self._size = 0
self._front = 0
Then, what if we call enqueue() when front is 6 and size is 1? In this case, the implicit rear will become 0 because (7 + 1) mod 8 = 0. The mod operation makes the pointer in arrays be circular.
It is only circular conceptually, and it is still a linear array. The implementation shares many ideas with Stack based on array in Stacks in Java.
A final problem to be addressed is to resize. As we have learned in Stacks in Java, we shall resize the underlying array if the size reaches to its capacity.
def enqueue(self, item):
# expand
if self.size() == len(self._data):
self._resize(2 * len(self._data))
avail = (self._front + self.size()) % len(self._data)
self._data[avail] = item
self._size += 1
We always double the array's size when the size of a queue reaches to its capacity. avail, computed through a mod operation, means, in fact, rear, the available position in the array.
def dequeue(self):
if self.is_empty():
raise NoElement('Dequeue from empty queue!')
# shrink (optional)
if self.size() <= len(self._data) // 4:
self._resize(len(self._data) // 2)
answer = self._data[self._front]
self._data[self._front] = None
self._front = (self._front + 1) % len(self._data)
self._size -= 1
return answer
The shrink operation is optional to save the memory space. Again, we update front through a mod operation. When the pointer shifts, it is a good practice to let it point to None for the sake of garbage collection.
The resize operation is a private method, and it is worthwhile to investigate how it works:
def _resize(self, capacity):
assert capacity > self.size()
old = self._data
self._data = [None] * capacity
walk = self._front
for i in range(self._size):
self._data[i] = old[walk]
walk = (1 + walk) % len(old)
self._front = 0
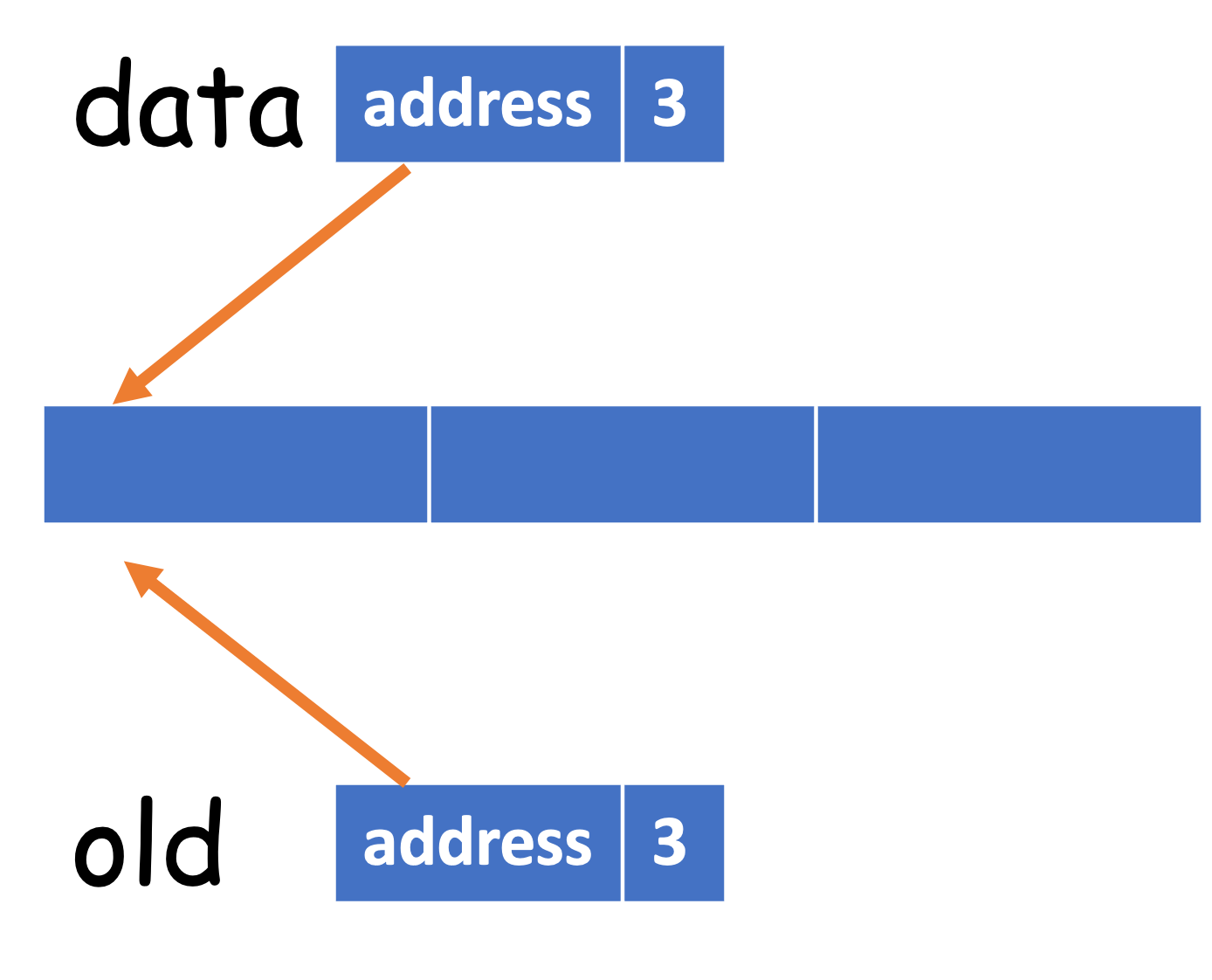
To understand it, we shall have a basic knowledge about the object model in Python:
When we create a list data, we essentially create a list and assigns the reference to data. So data is not the list itself, and it roughly has two parts: the address pointing to the list, and the size of the list.
data = [1, 2, 3]
old = data
If we add a new item to old, then data will also be updated:
old.append(4)
# [1, 2, 3, 4]
print(data)
Therefore, old and data refer to the same object, but with different names4. Now let's revisit the implementation of _resize(). After self._data = [None] * capacity is called, it becomes
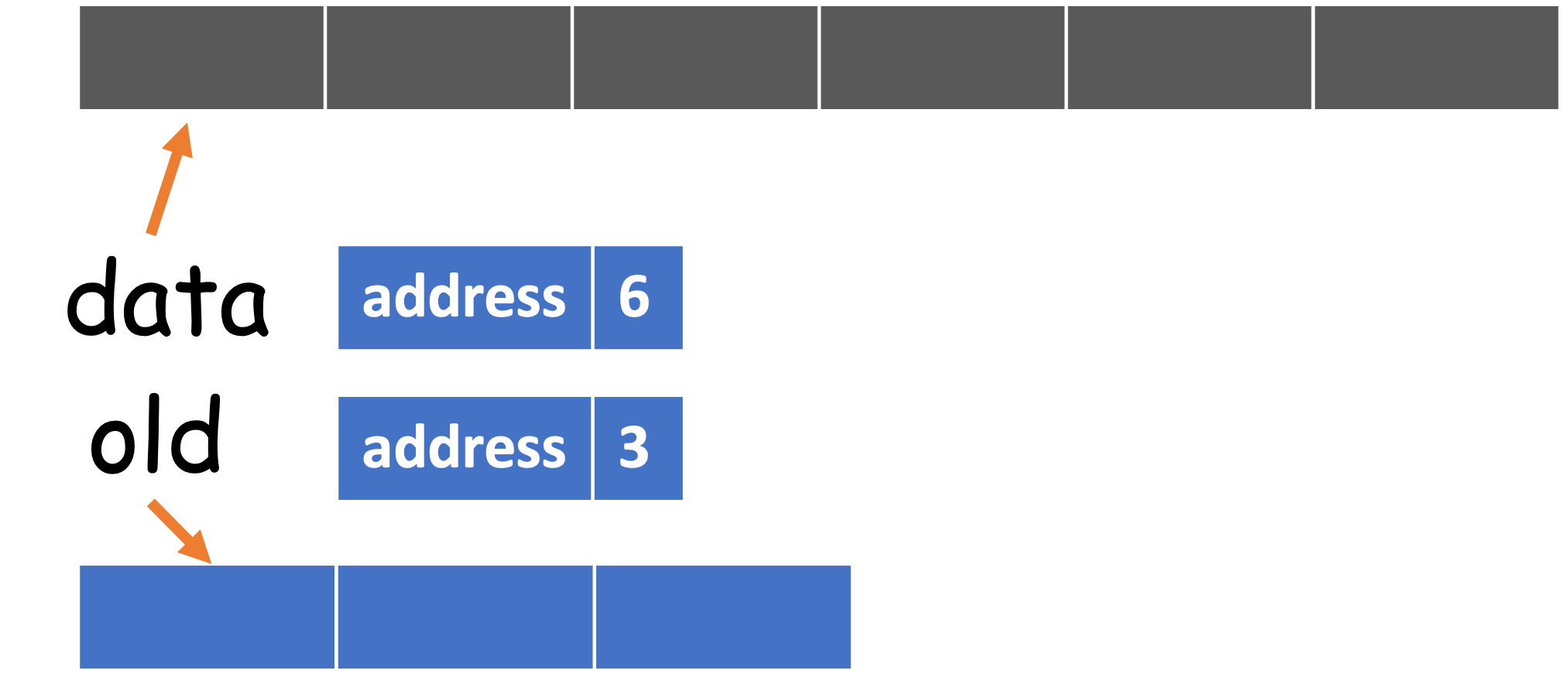
The next step is to copy from old[front..rear] to data[0.._size]. Of course, the range from front to near may be circular, so it should be computed through the mod operation.
The complete code can be found at circular_queue.py. Please try to implement an iterator for circular queues on your own before checking the code in GitHub.
A few notes on queues
When you need queues, please consider collections.deque, instead of implementing a new one from the scratch.
1 Like stacks, the time complexity of enqueue() is amortized.
2 To avoid the randomness brought by a single operation, we repeat it 20 times. Since 20 is much smaller than the size of queue, the measured time still makes sense.
3 Some designs assume that rear points to the last item in a queue. In this case, rear is -1 when the queue is empty.
4 https://towardsdatascience.com/python-memory-and-objects-e7bec4a2845