Case Study
As for the search/insert operation, we can summarize the time complexities of four common data structures we have learned:
| Algorithm (DAT) | Worst case cost after N inserts | Average case cost after N random inserts |
|---|---|---|
| sequential search (unordered linked list) | search: \(O(N)\) insert: \(O(N)\) | search: \(O(N)\) insert: \(O(N)\) |
| binary search (ordered array) | search: \(O(lg{N})\) insert: \(O(N)\) | search: \(O(lg{N})\) insert: \(O(N)\) |
| binary tree search (BST) | search: \(O(N)\) insert: \(O(N)\) | search: \(O(lg{N})\) insert: \(O(lg{N})\) |
| red-black BST | search: \(O(lg{N})\) insert: \(O(lg{N})\) | search: \(O(lg{N})\) insert: \(O(lg{N})\) |
Time efficiency
As we can see, the RBT is very efficient in terms of common operations, so it can be used fundamental building blocks in data structures underlying numerous applications:
- Many language standard collections, such as HashMap in Java and most implementations of STL in C++, are based on the red-black trees.
- Linux kernel uses the red-black tree in the memory management and task scheduling.
In what follows, we designed an experiment to compare ArrayList and a red black tree in terms of their search efficiency.
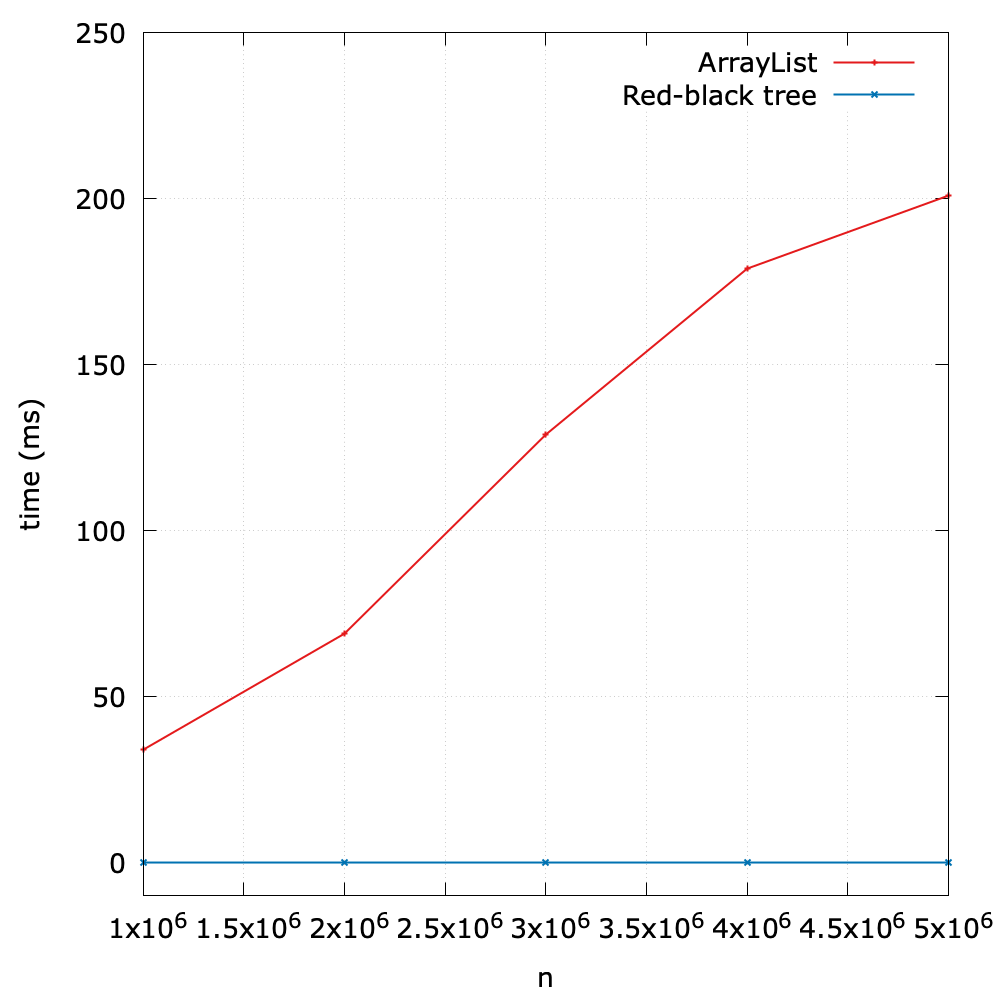
The results show the great superiority of the red-black tree.