PQ Implementation (1)
API
Priority queues are characterized by the remove the maximum and insert operations. A typical MaxPQ supports the following APIs:
insert(v): insert a key into the priority queuemax(): return the largest keydelMax(): return and remove the largest keyisEmpty(): is the priority queue empty?size(): number of keys in the priority queue
Any MaxPQ implementation is easily converted into a MinPQ implementation and vice versa.
Elementary implementations
The simplest priority-queue implementation is based on the code for stacks.
- insert: The same for
push()in the stack. - remove the maximum: exchange the maximum item with the item at the end, and then delete that one, as we did with
pop()for stacks.
Another approach is to add code for insert to keep the keys in the array in order. Thus, the largest element is always at the end.
| data structure | insert | remove maximum |
|---|---|---|
| ordered array | \(O(N)\) | \(O(1)\) |
| unordered array | \(O(1)\) | \(O(N)\) |
In addition, if we start with the linked list the linked list representation, the performance analysis is the similar.
As we can see, an ordered sequence is the prototypical eager approach, where we do as much work we can up front to make the latter operations efficient; unordered sequence is the lazy approach, where we defer doing work until sequences. But, both methods are unable to support all operations that take constant time.
How can we achieve a balance so that all operations are efficient? In the following section, we will learn another important data structure called heap that makes it possible.
Heap based implementation
Heap
A binary tree is heap-ordered if the key in each node is larger than or equal to the keys in that node's two children (if any).
From this definition, we can know that the largest key in a heap-ordered binary tree is found at the root. Different from a BST, duplicated keys are allowed in a heap-ordered binary tree.
Binary heap representation
We can use a linked representation for heap-ordered binary trees, as we did for a BST. But, it is particularly convenient to use a complete binary tree to represent it.
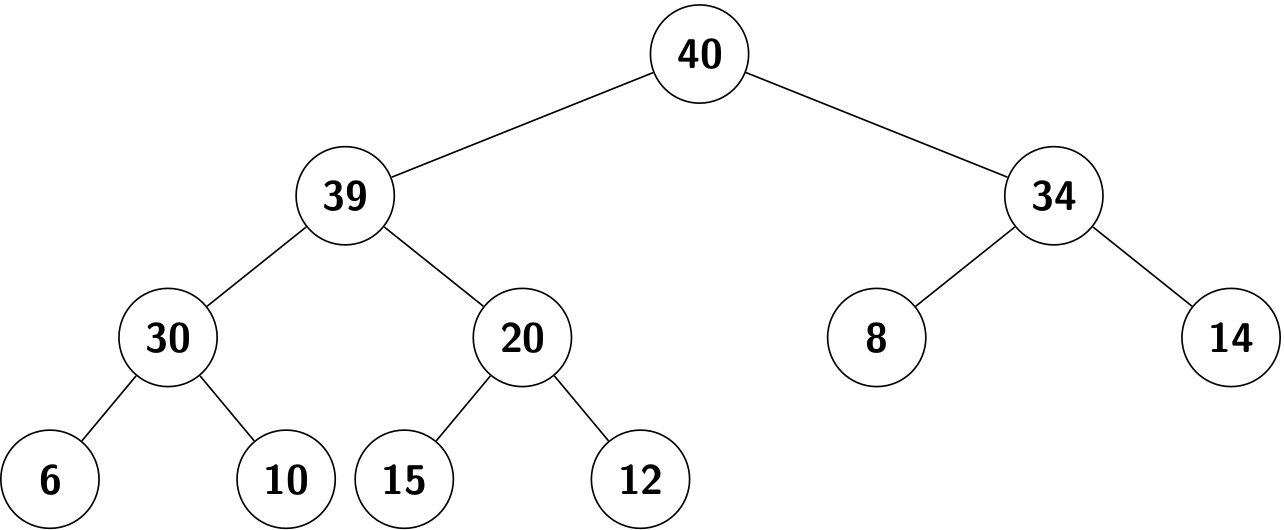
Complete binary tree provides the opportunity to use a compact array representation that does not involve explicit links. To be specific, we represent complete binary trees sequentially within an array by putting the nodes in level order, with the root at position 1, its children at positions 2 and 3, their children in positions 4, 5, 6 and 7, and so on.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a[i] | 40 | 39 | 34 | 30 | 20 | 8 | 14 | 6 | 10 | 15 | 12 |
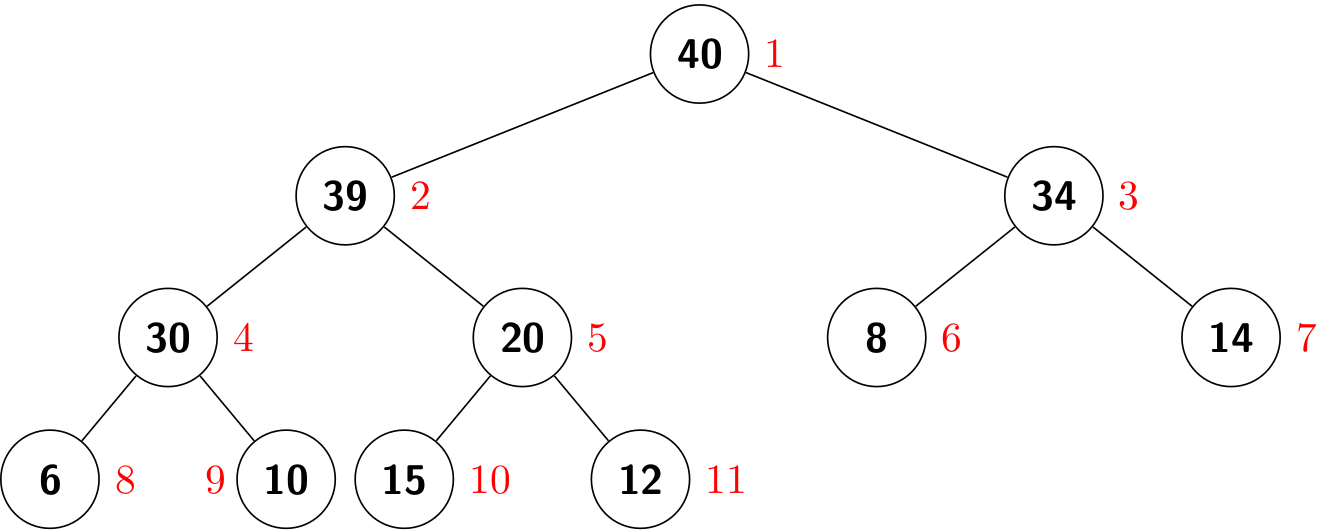
A binary heap is a collection of keys arranged in a complete heap-ordered binary tree, represented in level order in an array (not using the first entry).
Using this representation, the relationship between parent-children in a binary heap can be inferred by the position (i.e, index) in an array. For brevity, we will use heap when referring to a binary heap.
- The parent of the node in position k is position \(\lfloor k/2 \rfloor\).
- The two children of the node in position k are in positions 2k and 2k + 1.
It is easy to prove that the height of a complete binary tree of size N is \(\lfloor \lg{N} \rfloor\). Due to this property, we can design algorithms in guaranteed logarithmic time.
| data structure | insert | remove maximum |
|---|---|---|
| binary heap | \(O(\lg{N})\) | \(O(\lg{N})\) |